VMP逆向题分析

这道题其实不算难，主要是想记录一下vmp的解密流程。在解这道题之前，需要对vmp有一定了解，如果在此之前没有了解过的话，可以参考这篇文章¹，这篇文章基本上讲清楚了vmp的加密过程，甚至有兴趣的话还可以复现该帖子中讲述的vmp加密操作。

一开始拿到这种题我也是一头雾水，用kali远程调试进入初始化界面后，发现一个switch分支选择，如下图：

主程序界面

值得一提的是，我这里远程调试使用的是32位的linux_server文件，而这也为后续flag的非预期埋下了伏笔。进入界面后，发现switch分支选择一共有15个，分别代表了15个不同的操作，除了第15个操作不是函数以外，其它全是函数操作并都有参数进入，然后我理了一下这15个操作的逻辑，发现：

发现对值的操作有2、4、7（+、*、^四种操作）
而存入和取值的操作有1、8、9、10、11、15 （其中1、8、9、11、15是取值，10是存值）
关于地址的操作有11、13、14
关于值的比较有12
程序的开始是3
5、6是正确与错误的判断退出

到这里知晓了各个函数的作用，接下来就是根据参考帖子给出的思路，提取操作指令码。到这里我也明白了，vmp的题，你起码得知道程序整体运行逻辑，才有后面的逆向吧。提取后的操作指令如下图：

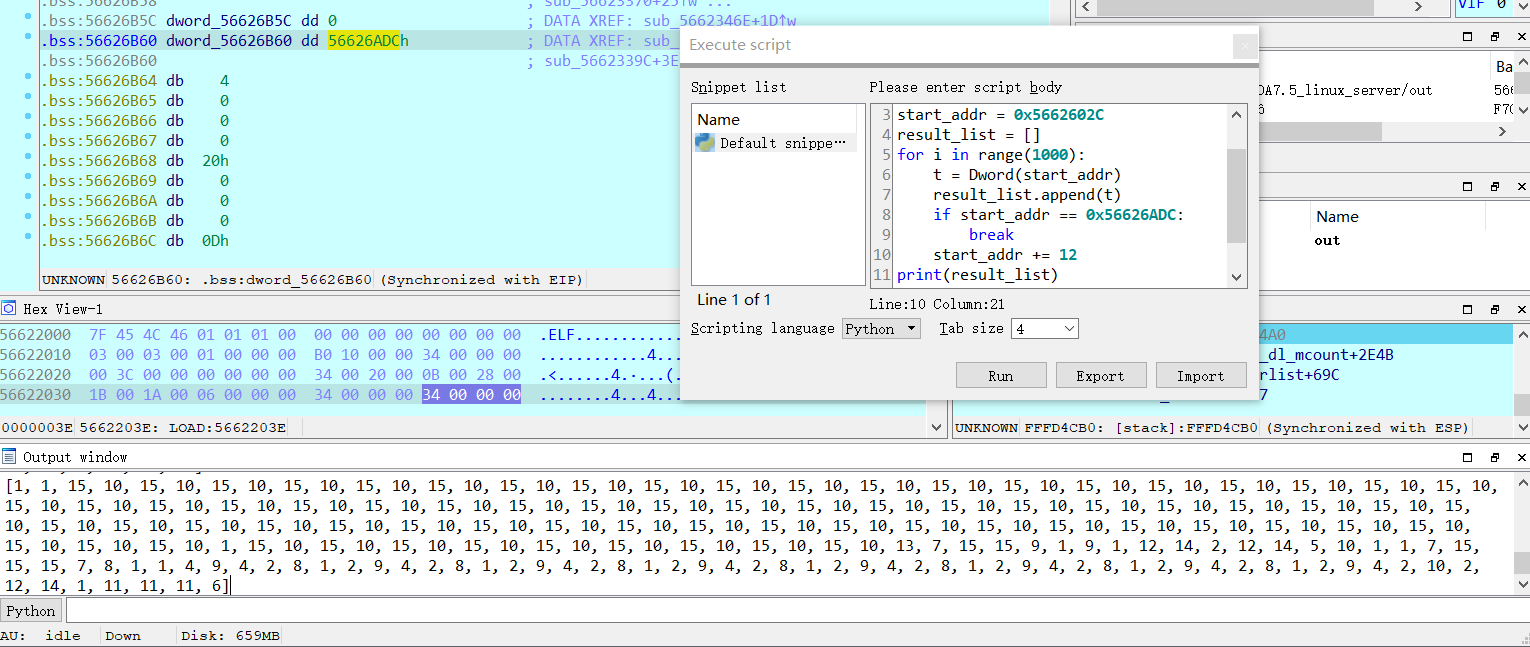
程序操作码

上面的脚本可以直接shift+F2弹出python脚本窗口后使用，脚本的目的是为了打印从基址开始的所有操作指令信息（该基址也就是3指令所在地址，而3指令指向的函数就是我们最开始的输入）。最后，提取到的指令码信息如下：

[3, 1, 1, 
15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 1, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 
13, 
 [7, 15, 15, 9, 1, 9, 1, 12, 14, 2, 12, 
  14, 5], 
 10, 1, 1, 7, 15, 15, 15, 
 7, 8, 1, 1, 4, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 10, 2, 12, 
14, 
 1, 11, 11, 11, 
 6]

我这里稍微整理了指令的逻辑，发现15和10这里的操作不用管，全部都是存取值操作；13以及14貌似是跳转，而中间重复出现的操作码貌似就是加密流程。但是提取到操作码之后我仍然不知道具体的逻辑，前后指令的衔接有什么关联，并且在实际动调中发现操作码运行到13后突然就飞到了10的位置，我还以为13后面跟着的7及其后面的操作码是没有用的（上面用[]框起来的指令信息），结果并不是，而是在暂时没有用到而已。后面我利用ida动调重新整理了一下逻辑，实际运行的操作码顺序如下：

[3, 
1, 1, 
15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 1, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 15, 10, 
13, 
 [7, 15, 15, 9, 1, 9, 1, 12, 14, 2, 12, 
  14, 5](?), 
10, 1, 1, 7, 15, 15, 15, 
 7, 8, 1, 1, 4, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12, 
14,
 7, 8, 1, 1, 4, 
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12, 
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14,
 7, 8, 1, 1, 4,
 9, 4, 2, 8, 1, 2, 
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 8, 1, 2,
 9, 4, 2, 10, 2, 12,
14, 
 1, 11, 11, 11, 
 [7, 15, 15, 9, 1, 9, 1, 12](!), 
14, 
 6]

可以看到加密一共执行了8轮，每一轮会重复进行8次加密操作，然后采用操作码12比较。到这里我一开始还认为12这里的比较是将输入的加密结果与正确的加密结果进行比较，但是后来发现并不是，12比较的是整个加密的循环次数。而我框起来的部分才是真正的加密判断。

我之所以能够清楚12是做循环判断，而框起来的部分是做加密判断，还是因为那篇帖子启示了我，后面我重新理了一遍逻辑。我发现，我没有将操作码后面跟着的两个参数值(参数1：基址+4、参数2：基址+8、操作码：基址+12)给跑下来，所以就导致我只能了解程序大概的流程，但是对于加密的细节等我还是未知，因此后面我又将操作码及其后面跟着的两个参数用脚本跑下来了，下面给出详细的操作码信息（我在后面作了详细解释）：

[3, 6, 0, 
 1, 1, 7, 
 1, 4, 6, 
 15, 0, 887631448, 10, 0, 0, # 这里面出现的前64个数据就是给定的要进行加密操作的数据
 15, 0, 853697698, 10, 0, 0, # 而最后8个数据则是通过我们的输入加密得到的结果
 15, 0, 461124623, 10, 0, 0, # 程序要比对的正确加密数据则是第64个数据后的8个数据
 15, 0, 245186321, 10, 0, 0, 
 15, 0, 646846967, 10, 0, 0, 
 15, 0, 1154116891, 10, 0, 0, 
 15, 0, 301809988, 10, 0, 0, 
 15, 0, 861868077, 10, 0, 0, 
 15, 0, 127091298, 10, 0, 0, 
 15, 0, 262294727, 10, 0, 0, 
 15, 0, 215708545, 10, 0, 0, 
 15, 0, 1654203685, 10, 0, 0, 
 15, 0, 53950545, 10, 0, 0, 
 15, 0, 700606238, 10, 0, 0, 
 15, 0, 1848475402, 10, 0, 0, 
 15, 0, 1879388492, 10, 0, 0, 
 15, 0, 1946291888, 10, 0, 0, 
 15, 0, 1927762797, 10, 0, 0, 
 15, 0, 1284115093, 10, 0, 0, 
 15, 0, 671092233, 10, 0, 0, 
 15, 0, 306073375, 10, 0, 0, 
 15, 0, 917468502, 10, 0, 0, 
 15, 0, 697240523, 10, 0, 0, 
 15, 0, 973896536, 10, 0, 0, 
 15, 0, 846872178, 10, 0, 0, 
 15, 0, 1595827532, 10, 0, 0, 
 15, 0, 945648588, 10, 0, 0, 
 15, 0, 860827719, 10, 0, 0, 
 15, 0, 336163122, 10, 0, 0, 
 15, 0, 924592411, 10, 0, 0, 
 15, 0, 873999272, 10, 0, 0, 
 15, 0, 152124282, 10, 0, 0, 
 15, 0, 1065431066, 10, 0, 0, 
 15, 0, 1022704734, 10, 0, 0, 
 15, 0, 1181311206, 10, 0, 0, 
 15, 0, 859976615, 10, 0, 0, 
 15, 0, 1966877851, 10, 0, 0, 
 15, 0, 81291526, 10, 0, 0, 
 15, 0, 2113741312, 10, 0, 0, 
 15, 0, 1458649115, 10, 0, 0, 
 15, 0, 735708505, 10, 0, 0, 
 15, 0, 727216090, 10, 0, 0, 
 15, 0, 1426344677, 10, 0, 0, 
 15, 0, 14041395, 10, 0, 0, 
 15, 0, 515709611, 10, 0, 0, 
 15, 0, 1475150066, 10, 0, 0, 
 15, 0, 1202930039, 10, 0, 0, 
 15, 0, 1875460324, 10, 0, 0, 
 15, 0, 1821127455, 10, 0, 0, 
 15, 0, 1333003323, 10, 0, 0, 
 15, 0, 2059534858, 10, 0, 0, 
 15, 0, 1867060019, 10, 0, 0, 
 15, 0, 1169256435, 10, 0, 0, 
 15, 0, 380318198, 10, 0, 0, 
 15, 0, 1911454699, 10, 0, 0, 
 15, 0, 1106722493, 10, 0, 0, 
 15, 0, 718999965, 10, 0, 0, 
 15, 0, 615938873, 10, 0, 0, 
 15, 0, 1450720726, 10, 0, 0, 
 15, 0, 471336241, 10, 0, 0, 
 15, 0, 997985349, 10, 0, 0, 
 15, 0, 631128684, 10, 0, 0, 
 15, 0, 1302688383, 10, 0, 0, 
 15, 0, 773211089, 10, 0, 0, 
 1, 5, 6, 
 15, 0, 1191123507, 10, 0, 0, 
 15, 0, 3998692370, 10, 0, 0, 
 15, 0, 2768718402, 10, 0, 0, 
 15, 0, 3824930148, 10, 0, 0, 
 15, 0, 2389687701, 10, 0, 0, 
 15, 0, 4087898125, 10, 0, 0, 
 15, 0, 3811936080, 10, 0, 0, 
 15, 0, 3319820756, 10, 0, 0, 
 15, 3, 450, 10, 3, 0, 
 13, 489, 0, # 跳转到操作码为10的前12字节的位置，489是偏移
 
 [7, 2, 2, 
 15, 9, 4, 
 15, 10, 32, 
 9, 3, 2, 
 1, 11, 0, 
 9, 5, 2, 
 1, 12, 0, 
 12, 11, 12, 
 14, 684, 0, 
 2, 2, 9, 
 12, 2, 10, 
 14, 459, 0, 
 5, 0, 0, ]
 
 10, 7, 0, # 索引7位置还是0，也就是等效于10 0 0
 1, 7, 6, 
 1, 3, 6,  # 把input此时的偏移量分别覆盖了7和3索引
 7, 2, 2,  # 通过异或操作对索引2赋值0
 15, 12, 4, # 它把4存入了索引12的位置（这个感觉像是个自增常量值4，类似于+=4）
 15, 13, 8, # 同理，它把8存入了索引13的位置
 15, 14, 64, # 把64存入了索引14的位置
 
 7, 10, 10, # 通过异或对索引10位置赋值0（但是每一轮相加的结果已经保存到了大数组input的后面，数字很明显，第二个0后开始的字节数组）
 8, 1, 0, # 取出input数组的第一位，即我们的输入的第一个4字节数据30303030，然后把值存入索引0的位置，即取出我们的第一个4字节输入然后存放到tmp（第二轮的循环开始会重新开始）
 1, 9, 0, # 然后把取出的值30303030存放到了索引9的位置
 
 1, 11, 2, # 接着把索引2的值存放到了索引11的位置（第二轮索引2为8）
 4, 11, 12, # 把索引11和12位置的数相乘最后存放到11，此时索引11是0，索引12是4，结果还是0（第二轮这里索引11值为32，因为索引12没变）
 
 9, 4, 11, # 取出索引11的值0以及索引4的值0x24计算地址（索引4也是没变，是个常量），最后取出input数组的第一位加密值34e82e58存放到索引0的位置，即取出第一位加密值然后存放到tmp
 4, 9, 0, # 把索引0和9位置的数相乘最后存放到9，此时索引0是加密值34e82e58，索引9的值是输入值30303030，相乘后最后存放到索引9，结果是a4b93080
 2, 10, 9, # 把索引10和9位置的数相加最后存放到索引10，此时索引9是a4b93080，索引10是0，最后存放到索引10，结果是a4b93080（感觉10代表的是sum）
 
 8, 1, 4, # 在0x24的基础加上4也就是0x28来作为input数组索引取值，然后把值存入索引为0的位置，即取出我们输入的第2个4字节组30303030存放到tmp
 1, 9, 0, # 然后把取出的值30303030存放到了索引9的位置，覆盖掉上一次相乘结果
 2, 11, 12, # 将索引11和12位置的数相加最后存放到索引11，此时索引11是0，索引12是4，结果变成了4，然后把结果存入11，即索引11的值从0变成了4（感觉像是在计算偏移，即进行i++操作）
 
 9, 4, 11, # 取出索引11的值4以及索引4的值0x24计算地址，最后取出input数组的第二位加密值32e264a2存放到索引0的位置，即取出第二位加密值存放到tmp
 4, 9, 0, # 把索引0和9位置的数相乘最后存放到9，此时索引0是加密值32e264a2，索引9是输入值30303030（已经是第2组了），相乘后存入索引9，结果是3bb13e60
 2, 10, 9, # 把索引9和10位置上的数相加后存入到索引10的位置，此时索引10是a4b93080，索引9位置是3bb13e60，结果是e06a6ee0
 8, 1, 8, # 在0x24的基础上加上8也就是0x2c来作为input数组索引取值，然后把值存入索引为0的位置，即取出输入的第3个4字节数组31313131存放到tmp
 1, 9, 0, # 把取出的值31313131存放到索引为9的位置，覆盖掉上一次相乘结果
 2, 11, 12, # *11和*12相加，结果存放到*11，*11=4，*12=4，结果*11=8，*12=4
 9, 4, 11, # 后面的计算过程与上面一致，唯一的问题是除了这样的小循环，还有大循环等着
 4, 9, 0, 
 2, 10, 9, 
 8, 1, 12, 
 1, 9, 0, 
 2, 11, 12, 
 9, 4, 11, 
 4, 9, 0, 
 2, 10, 9, 
 8, 1, 16, 
 1, 9, 0, 
 2, 11, 12, 
 9, 4, 11, 
 4, 9, 0, 
 2, 10, 9, 
 8, 1, 20, 
 1, 9, 0, 
 2, 11, 12, 
 9, 4, 11, 
 4, 9, 0, 
 2, 10, 9, 
 8, 1, 24, 
 1, 9, 0, 
 2, 11, 12, 
 9, 4, 11, 
 4, 9, 0, 
 2, 10, 9, 
 8, 1, 28, 
 1, 9, 0, 
 2, 11, 12, 
 
 9, 4, 11, 
 4, 9, 0, 
 2, 10, 9, 
 10, 10, 0, # 将索引10处的值10c33a07存入input数组中，此时input的偏移为0x14c，存入后偏移会+4，及变成了0x150
 2, 2, 13, # 将索引2处的值与索引13处的值进行相加，最后存入索引2处，此时索引2值为0，索引13值为8，相加结果为8，最后索引2处值会变成8
 12, 2, 14, # 将索引2以及14位置的值进行比较，此时索引2值为8，索引14值为64，此时值大小显然不一致（12其实是循环退出条件？）
 
 14, 510, 0,  # 将510与操作码基址相加，重新定位下一条指令地址，即进行条件判断后跳转，判断条件就是上面一个12判断结果是否为1，而12的判断结果则是计算循环次数是否达标。所以最后14判断不成立后会重新定位到操作码7的位置。
 
 1, 6, 7, # 加密循环结束后，将索引7处的值赋值到索引6处，此时索引7处值为偏移值332(0x14c)，而原先的索引6值为364(0x16c)，那么被赋值后索引6处值为0x14c
 11, 7, 0, # 然后利用全局偏移对input数组寻址，最后将寻到的值赋值给索引7处的位置，值为10c33a07，然后将偏移-=4，即向前移动，此时全局偏移为0x148，然后再判断此时索引值是否为8（此时索引为7），若不为8则正常运行
 11, 7, 0, # 再次利用全局偏移对input寻址，此时索引还是7，最后找到的值为0存入索引7，然后再次将偏移-=4，向前移动，此时全局偏移为0x144，由于此时索引仍不为8，所以程序正常运行
 11, 8, 0, # 再次利用全局偏移对input寻址，此时索引为8，然后将找到的值为1c2存入索引8，接着再将偏移-=4，向前移动，此时全局偏移为0x140，由于此时索引==8，所以程序会执行一个跳转，将操作基址与4*1c2相加，进行重定位，这个新地址指向新的操作码，也就是7，这个7与上面加密循环的7不一样，它执行的是下面的命令
 
 [7, 2, 2, # 将此时索引2处的值0x40(循环判断)通过异或计算重新清0，操作后索引2处的值为0
 15, 9, 4, # 将4赋值给索引9处
 15, 10, 32, # 将32赋值给索引10处，最后一轮的sum：cc55e5f9被覆盖
 9, 3, 2, # 取索引3处(0x14c)与2处(0)的值进行地址计算，最后将值10c33a07赋值到索引0处
 1, 11, 0, # 将10c33a07赋值到索引11处，原先的11处值为fc，此时索引11处的值为10c33a07
 9, 5, 2, # 取索引5处(0x124)与2处(0)的值进行地址计算，最后将值46ff1a33赋值到索引0处
 1, 12, 0, # 然后将值赋值到索引12处，原先的索引12处值为4，此时索引12处的值为46ff1a33
 12, 11, 12,] # 最后将索引11处的值与索引12处的值进行比较，结果正确返回1，错误返回0
 
 14, 684, 0 # 由于判断错误会执行重定位，基址加上传进来的参数684(0x2ac)，新地址指向的操作码为6，所以直接判断错误退出。(我猜测这里只要有一处判断没有通过就会退出，而不会执行后续判断)
 
 6]

跟着动调一遍，基本就理清了整个程序的运行逻辑，其中的加密逻辑非常简单，只用到了加乘操作。

整个程序会将用户的32字节输入变成8组4字节数据，然后用这8组字节数据与给定的64个4字节常量，按照8个一组一一对应的形式相乘再相加，这样一轮加密就结束了，最后将相加结果存入一个数组中，重复上述操作8次，最后数组会存入8个结果，最后会将数组值取出，与给定的正确加密结果比对，如果第一个值的比对没有成功，程序就会判断错误退出。

这就是整个程序的逻辑，下面给出我模拟的程序正向运行代码：

#include <stdio.h>
int main()
{
	// 模拟程序正向运行过程
	int test[] = {0x30303030, 0x30303030, 0x31313131, 0x31313131, 0x32323232, 0x32323232, 0x33333333, 0x33333333};	
	int code[] = {
		0x34E82E58, 0x32E264A2, 0x1B7C340F, 0x0E9D3F11, 0x268E19F7, 0x44CA6D1B, 0x11FD4144, 0x335F102D,
		0x7934262, 0x0FA24CC7, 0x0CDB7381, 0x62992525, 0x3373851, 0x29C2671E, 0x6E2D7F0A, 0x7005314C,
		0x74020EB0, 0x72E7536D, 0x4C8A0A95, 0x28000E09, 0x123E4F1F, 0x36AF7556, 0x298F0BCB, 0x3A0C7B58,
		0x327A3E72, 0x5F1E654C, 0x385D73CC, 0x334F3047, 0x14097132, 0x371C291B, 0x34182BA8, 0x9113B7A,
		0x3F81301A, 0x3CF53C5E, 0x466960E6, 0x334233A7, 0x753C2C9B, 0x4D86906, 0x7DFD2200, 0x56F1381B,
		0x2BDA0559, 0x2B586FDA, 0x55044AE5, 0x0D64133, 0x1EBD1AAB, 0x57ED00F2, 0x47B34177, 0x6FC940E4,
		0x6C8C331F, 0x4F74043B, 0x7AC2020A, 0x6F491333, 0x45B16FF3, 0x16AB31F6, 0x71EE7BEB, 0x41F73EBD,
		0x2ADB119D, 0x24B67B39, 0x56783DD6, 0x1C180531, 0x3B7C0C45, 0x259E426C, 0x4DA5727F, 0x2E1643D1
	};
	int test_encode[10]; 
	int i, j;
	int sum = 0;
	int c = 0;
	for(j = 0; j < 8; j++) {
		sum = 0; 
		for(i = 0; i < 8; i++) { // 小循环每次从头开始 
			sum += test[i] * code[c];
			c++;
		}
		test_encode[j] = sum;
	}
	for(int k = 0; k < 8; k++)
		printf("%x ", test_encode[k]);

	return 0;
}

我这里采用的输入是：

00000000111111112222222233333333

最后加密结果应该是：

0x10c33a07, 0x8cd09a46, 0x3584e781, 0xe41edd13,
0xb2cf4250, 0xef6c19f3, 0xb9ccc787, 0xcc55e5f9

根据正向脚本（不难看出正向加密过程其实就是线性方程组），逆向脚本也会很容易得出（我这里偷了懒，让GPT帮我用z3库写了脚本——z3库对解线性方程组有奇效），脚本如下：

from z3 import *
# 定义8个整数变量，代表 test 数组的8个元素
test = [BitVec(f'test_{i}', 32) for i in range(8)]
# 给定的 test_encode 数组
test_encode = [
    0x46FF1A33, 0xEE573412, 0xA5074A42, 0xE3FBCD64,
    0x8E6FBD95, 0xF3A8600D, 0xE3358750, 0xC5E071D4
]

# 0x10c33a07, 0x8cd09a46, 0x3584e781, 0xe41edd13,
# 0xb2cf4250, 0xef6c19f3, 0xb9ccc787, 0xcc55e5f9

# 给定的 code 数组
code = [
    0x34E82E58, 0x32E264A2, 0x1B7C340F, 0x0E9D3F11, 0x268E19F7, 0x44CA6D1B, 0x11FD4144, 0x335F102D,
    0x7934262, 0x0FA24CC7, 0x0CDB7381, 0x62992525, 0x3373851, 0x29C2671E, 0x6E2D7F0A, 0x7005314C,
    0x74020EB0, 0x72E7536D, 0x4C8A0A95, 0x28000E09, 0x123E4F1F, 0x36AF7556, 0x298F0BCB, 0x3A0C7B58,
    0x327A3E72, 0x5F1E654C, 0x385D73CC, 0x334F3047, 0x14097132, 0x371C291B, 0x34182BA8, 0x9113B7A,
    0x3F81301A, 0x3CF53C5E, 0x466960E6, 0x334233A7, 0x753C2C9B, 0x4D86906, 0x7DFD2200, 0x56F1381B,
    0x2BDA0559, 0x2B586FDA, 0x55044AE5, 0x0D64133, 0x1EBD1AAB, 0x57ED00F2, 0x47B34177, 0x6FC940E4,
    0x6C8C331F, 0x4F74043B, 0x7AC2020A, 0x6F491333, 0x45B16FF3, 0x16AB31F6, 0x71EE7BEB, 0x41F73EBD,
    0x2ADB119D, 0x24B67B39, 0x56783DD6, 0x1C180531, 0x3B7C0C45, 0x259E426C, 0x4DA5727F, 0x2E1643D1
]

# 将 code 数组转化为 8x8 的矩阵
A = [code[i*8:(i+1)*8] for i in range(8)]

# 初始化 Z3 求解器
solver = Solver()

# 添加约束条件：矩阵乘法 A * test = test_encode
for i in range(8):
    equation = Sum([A[i][j] * test[j] for j in range(8)]) == test_encode[i]
    solver.add(equation)

# 尝试求解
if solver.check() == sat:
    model = solver.model()
    result = [model[test[i]].as_long() for i in range(8)]
    print("找到符合条件的 test 数组:", [hex(x) for x in result])
else:
    print("未找到解。")

运行得到的结果是：（这里是小端序输出的结果，因为ida会将输入以小端序存储然后再进行计算）

0xe7616c66 0x6e69317b 0x9f724033 0xf4757145 
0xee4f6937 0x1269765f 0x31417574 0x3d457a49

最后将上面倒序一下就是正确的flag：

0x666C61E7 0x7B31696E 0x3340729F 0x457175F4 
0x37694FEE 0x5F766912 0x74754131 0x497A453D

得到的flag应该是：fla\xe7{1in3@r\x9fEqu\xf47iO\xee_vi\x12tuA1IzE=

显而易见，flag出现了不可显字符，我最开始解出flag也认为是我解错了，后来又把十六进制数据拿去动调修改验证，发现答案其实是正确的。初步猜测是因为运算是在int 32位上的，导致运算溢出然后求出非预期解了。（ok伏笔回收）

小结

小结一下，整个vmp的解密流程：

找到程序的操作码；
理清操作码并重新整理操作码顺序；
找到操作码后面跟着的指令信息（一般是操作码、指令1、指令2，三位一组的形式），并通过动调等手段整理逻辑；
最后就是将整理的逻辑尝试还原。

参考链接

https://mrwq.github.io/aggregate-paper/butian/那CTF，那VMre，那些事（一）/ ↩

小结

参考链接

Footnotes